1 - 背景
KNN:k近邻,表示基于k个最近的邻居的一种机器学习方法。该方法原理简单,构造方便。且是一个非参数化模型。
KNN是一个“懒学习”方法,也就是其本身没有训练过程。只有在对测试集进行结果预测的时候才会产生计算。KNN在训练阶段,只是简单的将训练集放入内存而已。该模型可以看成是对当前的特征空间进行一个划分。当对测试集进行结果预测时,先找到与该测试样本最接近的K个训练集样本,然后基于当前是分类任务还是回归任务来做对应的处理。KNN模型中有三个需要注意的地方:
1 - 距离度量的方法; 2 - K值的选择; 3 - 最后的判别决策规则。如上面第三个,较为简单的判别决策规则为:
1)分类任务,那么找这K个训练集样本中出现次数最多的那个标签作为该测试样本标签,如下图: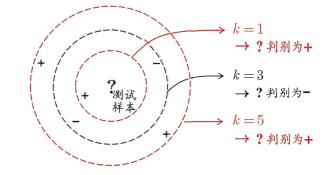
不过KNN正是因为基于K个近邻进行测量的方法,所以其出问题也就在这里,因为该模型不适合作为高特征维度下的选择。因为它会遇到维数灾难的问题。举个例子,假如当前数据集是均匀分布在一个D维特征的空间中的,假设我们需要计算测试样本\(x\)周边一个区域上的类别标签密度,那么我们期望基于足够大的区域范围的数据才能得到合理的结果,那么对应的边界长度公式为:
\[e_D(f) = f^{1/D}\] 也就是假如维度为\(D=10\),我们想评估10%的类别标签密度,那么每个维度上所需长度为\(e_{10}(0.1) = 0.8\),也就是我们需要每个维度上80%的长度范围内的数据,即使我们只需要估计1%的标签密度,我们每个维度上的长度也是\(e_{10}(0.01)=0.63\) 。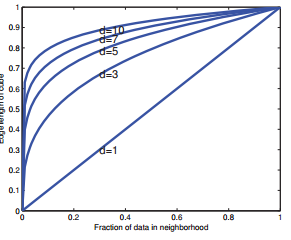
不过幸运的是, 有一个效应可以在一定程度上抵消维度灾难, 那就是所谓的“ 非均匀性的祝福”(blessing of nonuniformity) 。在大多数应用中, 样例在空间中并非均匀分布, 而是集中在一个低维流形manifold) 上面或附近。 这是因为数字图片的空间要远小于整个可能的空间。 学习器可以隐式地充分利用这个有效的更低维空间, 也可以显式地进行降维。[]
2 距离度量
KNN中最常用的方法就是欧式距离计算法,当然也有\(L_p\)距离和马氏距离等等。
假设样本的特征空间\(\chi\)是\(n\)维实数的向量空间\(\bf R^n\),\(x_i,x_j\in\chi\),$x_i=(x_i^{(1)}, x_i^{(2)}, ..., x_i^{(n)} ) \(,\)x_j=(x_j^{(1)},x_j^{(2)},...,x_j^{(n)})\(,那么\)x_i,x_j\(的\)L_p$距离定义为:\[L_p^{(x_i,x_j)}=(\sum_{l=1}^n|x_i^{l}-x_j^{l}|^p)^{\frac{1}{p}}\] 这里\(p\geq1\), 当\(p=2\)时,称为欧式距离; 当\(p=1\)时,称为曼哈顿距离; 当\(p=\infty\)时,是各个坐标距离的最大值,即:\[L_\infty(x_i,x_j)={max}_l|x_i^{(l)}-x_j^{(l)}|\]
3 K值选取
K值的选择会对KNN模型的结果产生重大影响。这就是一个模型选择问题。
模型选择:假设当前是一个KNN回归问题。现在是需要对点\(x_0\)进行\(\hat f_k(x_0)\)拟合,假设该样本来自函数\(Y=f(X)+\epsilon\), 这里\(E(\epsilon)=0\), 且\(Var(\epsilon)=\sigma^2\)。为了简化问题,假设训练样本中\(x_i\)的值是固定的,那么在测试样本点\(x_0\)的期望预测误差也叫做测试或泛化误差,如:\[\begin{eqnarray} EPE_k^{(x_0)} &=& E[(Y-\hat f_k(x_0))^2|X=x_0]\\ &=& \sigma^2+[Bias^2(\hat f_k(x_0))+Var(\hat f_k(x_0))]\\ &=& \sigma^2+[f(x_0)-\frac{1}{k}\sum_{l=1}^kf(x(l))]^2+\frac{\sigma^2}{k} \end{eqnarray}\] 第一项叫做不可避免的误差,是我们不可控制的,第二项和第三项是我们能够控制的,分别对应着模型的偏置和方差。偏置随着K变大而变大,方差随着K变大而变小。即K越大,模型越简单,K越小,模型越复杂: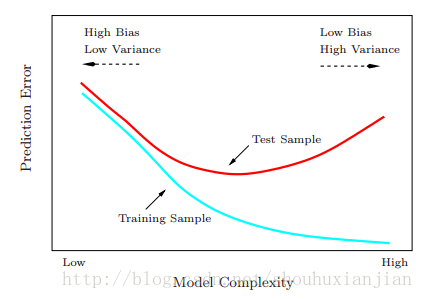
4 搜索优化
实现KNN模型时,主要考虑的还有个问题是如何对训练集的样本点进行快速的K近邻搜索。当特征空间维度太大,或者训练集样本点很多的时候特别重要。最基础的搜索方法就是线性搜索了,可想而知每个测试样本在比较时,都需要去计算一遍训练集的所有样本。效率着实不高。所以才需要量身定做的数据结构搜索方法。
4.1 - KD树
4.2 - Ball树
(待续)
参考资料: [] Machine Learning A Probabilistic Perspective [] 李航,统计学习方法 [] The Elements of Statistical Learning Data Mining, Inference, and Prediction (Second Edition) [] Pedro Domingos,A Few Useful Things to Know About Machine Learning [] 以叶子为数据的http://www.cnblogs.com/lysuns/articles/4710712.html []